BETA AND RISK-REWARD RATIO

Daily the TV channels and financial magazines spew forth terminology like risk reward ratio, beta, markets being efficient etc etc. A lot of people I meet, ask me these questions. What is beta? How does it help me in taking an investment decision? What are high beta stocks? When is risk reward ratio in my favour?

In 1952, Harry Markowitz a young graduate student of the University of Chicago published a paper in  The Journal of Finance, “Portfolio Selection”. That brief paper is today credited with the launching of  modern stock market theories and portfolio management as a mathematical science. Currently,  Markowitz is a professor of finance at the Rady School of Management, University of California, San Diego. He a recipient of the John von Neumann Theory Prize and the Nobel Memorial Prize in Economic Sciences.

His theory was that return and reward are inextricably linked. One can quantify the degree of risk that would be required for various levels of reward. He used standard deviation(SD) as a measure of risk. The further you are away from the standard deviation on the positive side, the greater is the risk and lower is the reward and vice versa.

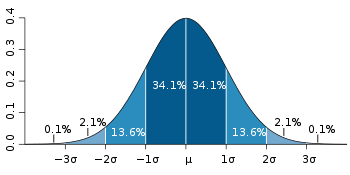
What is Standard Deviation? It is dispersion of the data from the “average” or mean. Usually a given set of data follows a “normal distribution of data”. If plotted on a curve, it will give a bell shaped curve.

Let me illustrate this by an example, in an exam taken by 100 students,  there are 68 students who score between 34 and 66 marks, 14 students who score between 67 and 84 marks, three students get between 85 and 96, one student gets 100, 13 students get less than 33 and one student gets 5 marks.

If I plot this data on a graph it will be like what is given above. When the teacher is asked, “What are the average marks scored by a student in your class?”  He replies 50. The average score of the class or mean (µ) is 50. The standard deviation (SD) is 17.

It means that 68% students should score between 33  (µ – SD=50-17)  and 67 marks (µ + SD=50-17). 95% students between 16 (µ – 2SD=50-34) and 84 marks (µ + 2SD=50+34).  And only 5% students are outside this range. The results of this class were very similar.

Take your mind back to school days. Pass marks were above 33 marks. The schools assumed that we would follow the normal distribution curve and only 16% students would be below that critical 33 mark line. And it was usually true !!! Check out the grading system in fauji courses.  It follows the bell shaped curve.

Going back to Markowitz, he propounded that if the markets or a particular stock is at a price of 2SD or 3SD away from its fair value, the risk of loss is more and reward is less and conversely if it is 2 or 3 SD below mean you may get rewarded handsomely as the risk is less.   But Markowitz did not take into account the decision maker, ie human being. Despite the risk reward ratio being in our favour, we do not take a financially prudent decision. Why was that so? This anomaly was captured by Kahneman & Tversky in their Prospekt Theory and they focused on Behavioural Economics.

In one of my earlier blogs I had explained this concept, When is the right time to invest in stocks?  The median or average of Indian Sensex is a PE multiple of 14 and its std devn  is 3. If the sensex is trading at SD  below the normal, as it was in Nov-Dec 2011, the risk reward ratio becomes in favour of the investor. The greater the deviation from the mean greater is the risk/reward.

In 1962, William Forsyth Sharpe a young PhD student approached Markowitz for guidance and in 1963, he published a dissertation, A Simplified Model for Portfolio Analysis. He postulated that every stock has a common relation with an underlying base factor. And if compared to that base, the risk can be quantified. For stocks, the best base is the complete stock market itself. If the stock market falls by 10% but Suzlon share price falls by 20%, logically and mathematically, it is a risky stock. Conversely, if Asian Paints falls only by 5%, it is less risky.  This variation in prices is also termed as volatility of prices. And Sharpe called this volatility measeure – beta factor. Beta (B) is the degree of correlation between the market as a whole and an individual stock price. If a stock falls or rises twice as fast as the markets, it will have a  B of 2. Thus, if the complete portfolio has a beta of 1.8, your portfolio is full of high risk stocks. You may gain high and lose high. Today, the Sharpe ratio is used to characterize how well the return of an asset compensates the investor for the risk taken, the higher the Sharpe ratio number the better.  Even mutual funds give out their Sharpe ratios.

Peter Bernstein, the author of the seminal work, “Against All Gods”,  studied Sharpe’s work in depth and concluded that the most efficient investment was to buy the whole stock market. But can we as individuals do that? Possibly Yes, practically No. What is the next best thing? Buy the Index or Nifty, through an Index fund, regularly for a long time and sell all your stock holdings when the markets are trading at 2 or 3 SD above normal and go meet your grandparents on a holiday.

And just as a reminder, the next time a teacher tells you, “Your child is an average child”, please correct him or her. Tell them, “My child’s marks may be “average” but my child is “unique”. There are no sigmas or standard deviations there.